Page 1 of 3
Conical bore and tone holes
Posted: Fri Jan 16, 2009 7:25 am
by Dan Mozell
For all your makers and tweakers out there.
Anyone know how to calculate tone hole sizes and locations for CONICAL bores?
I thought I'd experiment with a poor man's version of a conical bore, modifying a pvc or cpvc tube with liquid plastic to create a pseudo conical bore.
Re: Conical bore and tone holes
Posted: Fri Jan 16, 2009 11:00 am
by Gregrussell
Dan Mozell wrote:For all your makers and tweakers out there.
Anyone know how to calculate tone hole sizes and locations for CONICAL bores?
I thought I'd experiment with a poor man's version of a conical bore, modifying a pvc or cpvc tube with liquid plastic to create a pseudo conical bore.
Hi Dan,
I use 1.618 as a division tool.....I first start by cutting the tube til the bell note is reached. then measure from the labium to the end of your tube. divide by 1.618 by 1.618 by 1.618....this will layout the nodes of your tube, layout your hole based on your nodes...you can see how the hole gets bigger closer to the node....Initially I choose my locations and reem the holes out until my hole size reaches the desired note....once I have the hole sizes I then choose a drill bit closest to the sizes uncovered by reeming. cover the holes you drilled with tape....turn your tube 180 degrees and drill new holes from the bottom up......and adjust new holes up or down to reach desired note....be prepared to scrap a tube or two...
I hope this helps...this is The way I do it......and it works, I don't trust magic formula's myself....It all comes down to customizing chaos for me

cheers,
Greg
Re: Conical bore and tone holes
Posted: Fri Jan 16, 2009 11:37 am
by Feadoggie
I hope this helps...this is The way I do it......and it works, I don't trust magic formula's myself....It all comes down to customizing chaos for me



It is all magic in the end though! That's a pretty reasonable approach too, Greg.
Feadoggie
Re: Conical bore and tone holes
Posted: Fri Jan 16, 2009 1:37 pm
by Protean
Ye gods, how I want to make a whistle!
(Sorry, somewhat off topic, I know. But reading Greg's post, it just sounds like a lot of fun to me!

)
Re: Conical bore and tone holes
Posted: Sat Jan 17, 2009 1:49 pm
by highwood
I know of no online sources for calculating holes in a conical instrument. Nederveen's book ('acoustical aspects of woodwind instrument') has the equations for both cylindrical and conical bores and much more, which include the first order approximations used by the spreadsheets that can be found online by, or based on Pete Kosel's work which are I believe also are used by the flutomat calculator.
So as not to mislead you the book does not give you a packaged solution - it is not a how to book!
A couple refinements to my cylindrical whistle design and I'm going to move on to trying a conical design, and diving into the math followed by almost certainly many prototypes.
Bill
Re: Conical bore and tone holes
Posted: Sat Jan 17, 2009 5:34 pm
by hans
Gregrussell wrote:I use 1.618 as a division tool.....I first start by cutting the tube til the bell note is reached. then measure from the labium to the end of your tube. divide by 1.618 by 1.618 by 1.618....this will layout the nodes of your tube, layout your hole based on your nodes...you can see how the hole gets bigger closer to the node....Initially I choose my locations and reem the holes out until my hole size reaches the desired note....once I have the hole sizes I then choose a drill bit closest to the sizes uncovered by reeming. cover the holes you drilled with tape....turn your tube 180 degrees and drill new holes from the bottom up......and adjust new holes up or down to reach desired note....be prepared to scrap a tube or two...
Greg - I wish I could understand your procedure, and the rational behind it. All I know is that dividing by 1.618 is the golden ratio, but i have no idea what that has to do with nodes and hole sizes

~Hans
Re: Conical bore and tone holes
Posted: Sat Jan 17, 2009 5:48 pm
by hans
highwood wrote:I know of no online sources for calculating holes in a conical instrument. Nederveen's book ('acoustical aspects of woodwind instrument') has the equations for both cylindrical and conical bores and much more, which include the first order approximations used by the spreadsheets that can be found online by, or based on Pete Kosel's work which are I believe also are used by the flutomat calculator.
Peter Hoekje's Exel spreadsheet gives the possibility to set the tube diameter for each tone hole location, so you can use it for a tapered bore.
Pete Kosel's Flutomat javascript form page does not give that option and can be used only for cylindrical bores.
Both I find to be not very precise, but good for a first approximation.
Note that for a whistle design you need quite a different length correction for the whistle window than for the flute embouchure hole, i.e. the formula used for calculating the correction for the emb. hole needs adjustment.
~Hans
Re: Conical bore and tone holes
Posted: Sat Jan 17, 2009 7:35 pm
by Gregrussell
Greg - I wish I could understand your procedure, and the rational behind it. All I know is that dividing by 1.618 is the golden ratio, but i have no idea what that has to do with nodes and hole sizes

~Hans[/quote]
Pluck a string on a guitar, and search for the harmonics by lightly touching the string without making it touch the frets and you will find pure Fibonacci and 1.618 relationships. A guitar string is not much different then the column of air in your whistle....Hence the fret board is also layed out this way....no wonder they call the number "golden"
Re: Conical bore and tone holes
Posted: Sat Jan 17, 2009 8:38 pm
by Gregrussell
hans wrote:Gregrussell wrote:I use 1.618 as a division tool.....I first start by cutting the tube til the bell note is reached. then measure from the labium to the end of your tube. divide by 1.618 by 1.618 by 1.618....this will layout the nodes of your tube, layout your hole based on your nodes...you can see how the hole gets bigger closer to the node....Initially I choose my locations and reem the holes out until my hole size reaches the desired note....once I have the hole sizes I then choose a drill bit closest to the sizes uncovered by reeming. cover the holes you drilled with tape....turn your tube 180 degrees and drill new holes from the bottom up......and adjust new holes up or down to reach desired note....be prepared to scrap a tube or two...
Greg - I wish I could understand your procedure, and the rational behind it. All I know is that dividing by 1.618 is the golden ratio, but i have no idea what that has to do with nodes and hole sizes

~Hans
Hans, here is a picture of a generation d I missed the "G" ohwell

...but thats ok..it's just a rough diagram showing the divisions....I also use this ratio for my wind way calculations
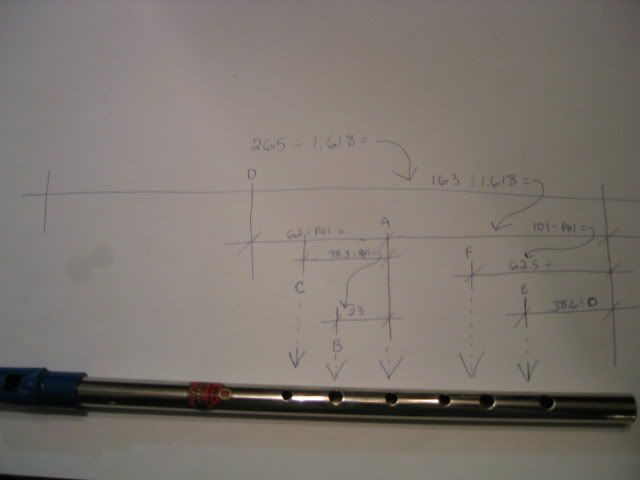
Re: Conical bore and tone holes
Posted: Sat Jan 17, 2009 9:30 pm
by jiminos
thank you for the pic, greg. even without the G, it is pretty easy to understand. very cool. so... pardon my ignorance, but where did the 1.618 come from? when i make my flutes i use a much different way of calculating based on the 12 half tones from root to octave that make up the chromatic scale.
be well,
jim
Re: Conical bore and tone holes
Posted: Sat Jan 17, 2009 9:53 pm
by Gregrussell
jiminos wrote:thank you for the pic, greg. even without the G, it is pretty easy to understand. very cool. so... pardon my ignorance, but where did the 1.618 come from? when i make my flutes i use a much different way of calculating based on the 12 half tones from root to octave that make up the chromatic scale.
be well,
jim
Maybe the question is, "where did we come from" and "what are we doing here?"

I was trained as a professional trades person, In my everyday work I always found this number. I also build violins and found every key measurement was based on 1.618 ...strange? not at all!!! turns out the construction of our bodies are inherent to this ratio....and possibly what we find pleasing has to do with who we are and how we're made!...The shape of 1.618 is a pentagram, the inner ear is also shape to this natural phenom...don't make me draw another picture!!

!
Check this out....
http://goldennumber.net/music.htm
http://goldennumber.net/dna.htm
http://goldennumber.net/solarsys.htm
Re: Conical bore and tone holes
Posted: Sun Jan 18, 2009 1:33 pm
by jiminos
well, isn't that just cool as hell! absolutely fascinating! thank you very much for posting the links.
the geek/nerd in me is jumping up and down like a little child in a candy store.
be well,
jim
Re: Conical bore and tone holes
Posted: Sun Jan 18, 2009 2:03 pm
by GordonH
I am just having a short break from making one of these:
http://www.ehhs.cmich.edu/~dhavlena/low-d.htm
using one inch diameter thin wall aluminium allow tubing and a bit of broom handle.
Within an hour I had a tube sounding a low D!
Making the holes will be for tomorrow, but I think using a tapered reamer is the way to go for fine adjustment of sizes.
The guy who wrote that article says there is no difference in spacing between conical and cylindrical bore.
Re: Conical bore and tone holes
Posted: Mon Jan 19, 2009 4:04 pm
by hans
Gregrussell wrote:Pluck a string on a guitar, and search for the harmonics by lightly touching the string without making it touch the frets and you will find pure Fibonacci and 1.618 relationships. A guitar string is not much different then the column of air in your whistle....Hence the fret board is also layed out this way....no wonder they call the number "golden"
I don't think this is the case.
On a guitar the second harmonic is the fifth above the octave (first harmonic) and it occurs when dividing the string by three. Lightly touching the string one third way, so two thirds of the string remain, will sound the first harmonic (octave) of the fifth, i.e the same note which is fingerd a fifth above octave with a third of the string length. Two thirds is 0.666..., not 0.618 (golden proportion; 1/1.618=0.618).
Pressure nodes and anti-nodes in a flute or whistle are located similar, with the slight difference that the sounding air column is a little longer than the tube.
See
flute acoustics. The pressure node in a flute for the first harmonic (octave) is located half way down the tube length, the pressure anti-nodes are located ca. one quarter and three quarters along the tube. The Golden Proportion has no bearing.
I have studied Fibonacci numbers and the Golden Proportion in nature, and find these to be fascinating aspects of naturally evolved efficient design, but when it comes to determine acoustically efficient location for flute tone holes I rather follow the maths of logarithmic divisions. To locate tone holes in places we organically evolved beings can reach comfortably with our fingers I then need to alter hole diameters (shift hole up: make it smaller; shift hole down: make it bigger) in a precise mathematical fashion which takes account of all the holes, or simply empirically by trial and error.
The resulting spread of holes has again nothing to do with the Golden Proportion. I aim to have somewhat equal distances between holes 1, 2 and 3, as between holes 4, 5 and 6. This is of course a big "somewhat", and usually a compromise between equal spacing and acoustically efficient spacing is best.
Great fun, all of this!
~Hans
Re: Conical bore and tone holes
Posted: Mon Jan 19, 2009 4:28 pm
by Gregrussell
hans wrote:Gregrussell wrote:Pluck a string on a guitar, and search for the harmonics by lightly touching the string without making it touch the frets and you will find pure Fibonacci and 1.618 relationships. A guitar string is not much different then the column of air in your whistle....Hence the fret board is also layed out this way....no wonder they call the number "golden"
I don't think this is the case.
On a guitar the second harmonic is the fifth above the octave (first harmonic) and it occurs when dividing the string by three. Lightly touching the string one third way, so two thirds of the string remain, will sound the first harmonic (octave) of the fifth, i.e the same note which is fingerd a fifth above octave with a third of the string length. Two thirds is 0.666..., not 0.618 (golden proportion; 1/1.618=0.618).
Pressure nodes and anti-nodes in a flute or whistle are located similar, with the slight difference that the sounding air column is a little longer than the tube.
See
flute acoustics. The pressure node in a flute for the first harmonic (octave) is located half way down the tube length, the pressure anti-nodes are located ca. one quarter and three quarters along the tube. The Golden Proportion has no bearing.
I have studied Fibonacci numbers and the Golden Proportion in nature, and find these to be fascinating aspects of naturally evolved efficient design, but when it comes to determine acoustically efficient location for flute tone holes I rather follow the maths of logarithmic divisions. To locate tone holes in places we organically evolved beings can reach comfortably with our fingers I then need to alter hole diameters (shift hole up: make it smaller; shift hole down: make it bigger) in a precise mathematical fashion which takes account of all the holes, or simply empirically by trial and error.
The resulting spread of holes has again nothing to do with the Golden Proportion. I aim to have somewhat equal distances between holes 1, 2 and 3, as between holes 4, 5 and 6. This is of course a big "somewhat", and usually a compromise between equal spacing and acoustically efficient spacing is best.
Great fun, all of this!
~Hans
thanks hans....if it works it works, your much smarter then me....

carry on,
Greg
